Lecture 38: Case Study#
Implementation - Monte Carlo Simulation Framework#
The Monte Carlo Simulation framework enables use of the Adaptive Large Neighbourhood Search (ALNS) algorithm to optimise and simulate the strategic, tactical, and operational decision-making associated with Dynamic-Stochastic Multi-Echelon Capacitated Location Routing Problem with Time-Windows (DS-ME-C-LRP-TW). Specifically, at the strategic level, the framework utilises the ALNS algorithm to configure the distribution structure for the planning horizon to optimally meet the anticipated customer demand over this period. Subsequently, at the tactical level, the Monte Carlo Simulation framework simulates each working day sampled from the planning horizon, configuring daily distribution operations using the ALNS algorithm to optimally service the daily stochastic customer demand. Finally, at the operational level, the framework deploys the ALNS algorithm to fine-tune the daily distribution operations for each simulated working-day to optimally cater to the dynamic customer demand arriving through the day, requesting for service by the end of the day.
Empirical Results - Los Angeles#
Without loss of generality, the case study here considers an e-retailer with a 1% market share, catering to a dynamic and stochastic customer demand in Los Angeles through demand-responsive expedited delivery service facilitated by ITS (see Figure 1 and Figure 2).
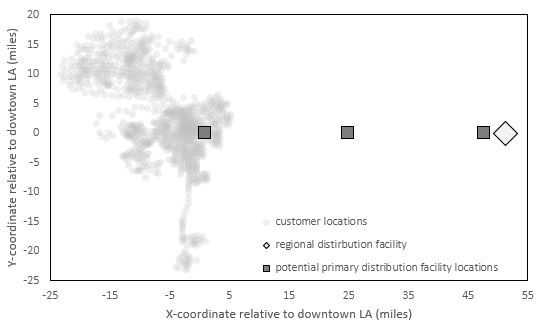
Figure 1. Last-mile distribution environment in Los Angeles
This e-retailer plans to establish operations for a planning horizon of 10 years, with each year consisting of 330 working days and 12 working hours (8 AM–8 PM), limited to 9 hours per staff member. Thus, to optimise the strategic, tactical, and operational decision-making for this e-retailer, the case study here employs the Monte Carlo framework.
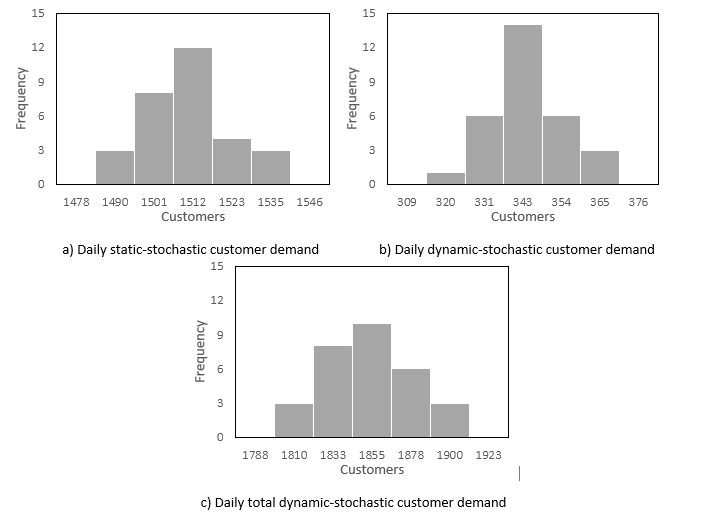
Figure 2. Los Angeles customer demand
Specifically, the framework optimises the strategic aspects of the distribution structure to meet projected customer demand over the 10 years. This renders a primary distribution facility positioned in downtown Los Angeles supported with a fleet of 20 diesel trucks responsible for delivering packages to the customers. The framework then simulates a representative sample of 30days from the planning horizon, optimising daily distribution operations (tactical aspects) to serve the daily stochastic customer demand. For each of simulated day, the framework fine-tunes the operational aspects of last-mile distribution to optimally cater to the dynamic customer demand arriving randomly and uniformly until 2 PM (cut-off time), amounting to 20% of the total demand (degree of dynamism). Together, this renders an average total cost of USD 4.32 per package, which includes a fixed cost of USD 0.94 and an operational cost of USD 3.38, per package. Notably, a significant portion of this total cost, amounting to $0.45 per package, stems from catering to the dynamic customer demand. Figure 3 showcases convergence plots and optimal solutions for the three decision-making levels.
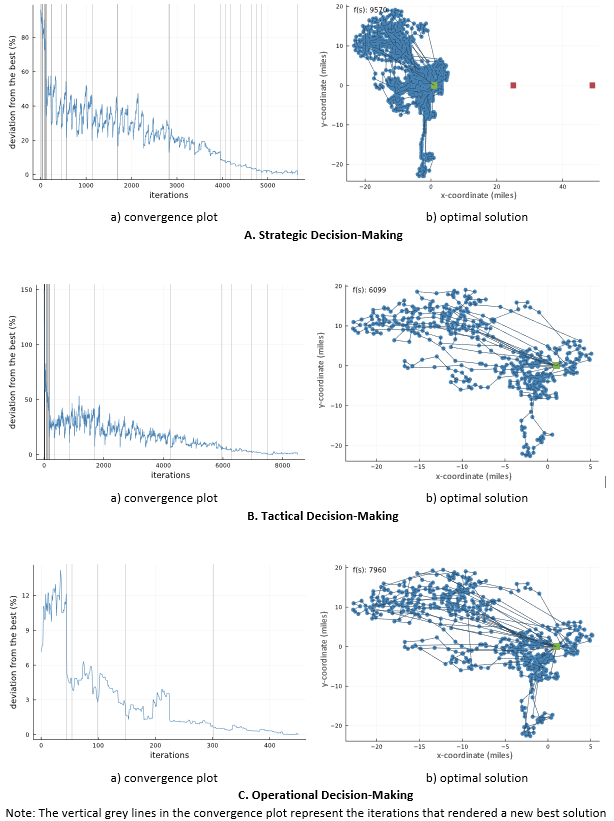
Figure 3. Empirical Results – Monte Carlo Simulation Framework