Lecture 28: Metaheuristics#
Note
Formed by combining the Greek prefix meta, implying high-level, and heuristic from the Greek heuriskein or euriskein which means to search, metaheuristics are high-level search frameworks. Here, high-level refers to an abstract problem-solving strategy, while search refers to exploration and exploitation of solution landscape. To put it simply, metaheuristics are are flexible algorithmic frameworks designed to find near-optimal solutions to complex optimization problems.
Introduction#
Modern transportation systems leverage advanced technologies to enable data-driven decision-making for optimal performance of the transportation systems. Its applications span a diverse range of domains, including resourceful parking space allocation (parking system optimisation), optimal path-planning for autonomous vehicles (vehicle navigation optimisation), coordinated and synchronised transit operations planning (transit timetable and schedule optimisation), responsive management of on-demand transportation services (dial-a-ride problem), efficient delivery route design (vehicle routing problem), and effective traffic management (traffic signal optimisation, traffic assignment problem). These applications underscore the vital role of modern transportation systems in facilitating urban mobility which is characterised by uncertainty (dynamic and stochastic information) as well as high-dimensional decision space, thus necessitating use of advanced computational methods.
To this end, metaheuristic algorithms have emerged as powerful tools to establish adaptive frameworks that can render near-optimal solutions to these complex transportation problems. Metaheuristics are mechanisms that guide solution search through solution landscape exploration (diversification) and exploitation (intensification). They can be broadly categorised as local search heuristics and population-based heuristics. Notably, local search heuristics iteratively refine solution by exploring and exploiting neighbourhoods of a solution to develop high-quality solution. On the other hand, population-based heuristics iteratively refine a population of solutions by leveraging interaction between different solutions to comprehensively explore and exploit the solution landscape, and thus develop high-quality solutions. Together, these metaheuristic procedures offer a flexible yet robust approach to solving complex optimisation problems inherent to modern transportation systems.
Example#
Parking System Optimisation#
San Francisco DownTown has \(n\) unique parking lots, each with a total of \(m_i\) number of parking spaces available. How should the parking space be allocated such that each parking lot has an equitable usage?
Warning
dynamic and stochastic uncertainty: parking demand varies based on factors like time of day (dynamic) as well as weather, road closures, and special events (stochastic), making optimal allocation difficult.
high-dimensional decision space: a combinatorial number of potential solutions exist for this problem.
Transit TimeTable Optimisation#
Chennai Metro Rail (CMRL) plans to redevelop its timetable to better serve its passengers with an efficient service. How should CMRL design daily train timetable such that the total passenger wait time is minimised?
Warning
dynamic and stochastic uncertainty: passenger demand varies due to weather-related factors, special events, etc. (stochastic) as well as by the time of the day, day of the week, month of the year, etc. (dynamic).
high-dimensional decision space: designing train schedules across multiple routes, each with varying demand creates a vast search space of feasible timetables.
Vehicle Routing Problem#
A logistics company in Mumbai must deliver parcels to \(n\) locations in a city using \(m\) delivery vehicles. If each vehicle has a capacity of \(q\) packages and a time window fo \(t\) hours to complete the deliveries, how should the vehicles make delivery such that the total distance travel is minimised?
Warning
dynamic and stochastic uncertainty: often customer location and demand is stochastic and may also be dynamic, arrving periodically in the planning horizon.
high-dimensional decision space: there exist at least \(n!\) possible solutions to this problem; moreover, practical applications involve a huge number of delivery points with time-dependent operational variables.
Traffic Signal Optimisation#
An intersection in Delhi has \(n (n \le 6)\) incoming roads. What should be the green light interval logic for each direction such that the total intersection throughput is maximised?
Warning
dynamic and stochastic uncertainty: traffic volumes are stochastic (vary due to weather, road closures, sport/concert events, etc.) and dynamic (vary through the time of the day, day of the week, month of the year, etc.).
high-dimensional decision space: signal timing optimization across multiple phases, directions, and periods can creates a vast number of possible timing configurations; further, real-world signal optimization requires processing large amounts of historical vehicle flows to assess traffic patterns.
Table 1. Applications of Local Search and Population-Based Metaheuristics in modern transportation systems
Application |
HC |
TS |
TA |
SA |
ILS |
VNS |
EC |
SI |
|---|---|---|---|---|---|---|---|---|
Parking System Optimisation |
✗ |
✗ |
✗ |
✗ |
✗ |
✗ |
✓ |
✓ |
Vehicle Navigation Optimisation |
✗ |
✗ |
✗ |
✓ |
✓ |
✗ |
✓ |
✓ |
Transit Operations Optimisation |
✗ |
✗ |
✓ |
✓ |
✗ |
✗ |
✓ |
✓ |
Dial-a-Ride Problem |
✗ |
✓ |
✗ |
✓ |
✗ |
✓ |
✓ |
✓ |
Vehicle Routing Problem |
✗ |
✓ |
✗ |
✓ |
✓ |
✓ |
✓ |
✓ |
Traffic Signal Optimisation |
✓ |
✗ |
✗ |
✗ |
✓ |
✗ |
✓ |
✓ |
Traffic Assignment Problem |
✗ |
✗ |
✗ |
✓ |
✗ |
✗ |
✓ |
✓ |
Legend:
HC: Hill Climb
TS: Tabu Search
TA: Threshold Accepting
SA: Simulated Annealing
ILS: Iterative Local Search
VNS: Variable Neighbourhood Search
EC: Evolutionary Computation
SI: Swarm Intelligence
Applications#
Vehicle Navigation Optimisation#
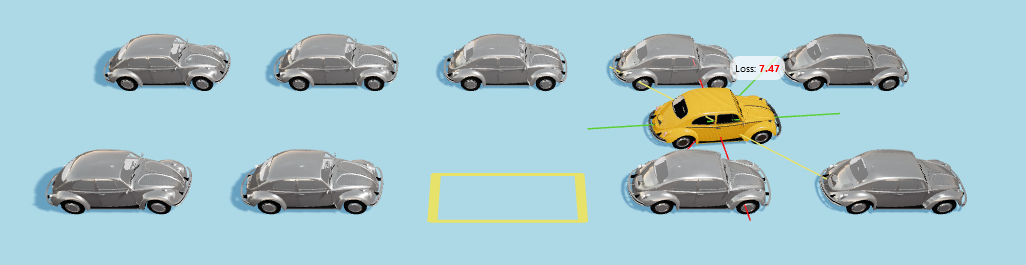
Figure 1. Self-Parking Car Simulation
The Self-Parking Car Evolution Simulator is an interactive tool designed to demonstrate the principles of genetic algorithms through a transportation-related use case. It simulates the evolution of virtual cars, progressively enhancing their ability to perform self-parking maneuvers over multiple generations. By mimicking the process of natural selection, the simulator evaluates each car based on its parking performance, selecting the most successful designs to create subsequent generations. As the simulation progresses, the algorithm optimizes key parameters such as speed, turning angle, and stopping accuracy, enabling the cars to refine their parking skills. With each new generation, the cars demonstrate increasingly effective solutions, providing a compelling visual representation of the evolutionary process.
Vehicle Design Optimisation#
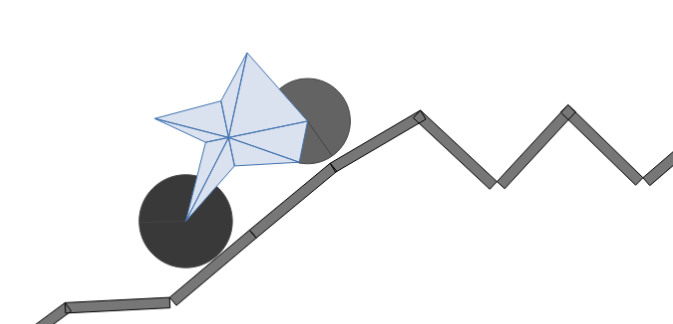
Figure 2. Generative Car Simulation
The Generative Car Simulator is an interactive application designed to illustrate the power of genetic algorithms through the evolution of vehicle designs. It simulates the process of natural selection to develop efficient two-wheeled car shapes capable of navigating challenging terrains. Over successive generations, the simulator optimizes various design features, such as the chassis shape, wheel size, wheel density, and wheel placement, improving the cars’ performance in the simulated environment. At its core, the simulator evaluates each car based on its ability to travel the farthest distance across a dynamic and progressively difficult terrain. The best-performing cars are selected to “reproduce,” passing their genetic traits onto the next generation with slight mutations. This evolutionary process results in cars that adapt better to the given challenges over time.