Lecture 21: Least-Cost Path Problem

Lecture 21: Least-Cost Path Problem#

General Description#

For a network modeled as a directed graph \(G=(N,A)\), with \(N\) and \(A\) representing the set of nodes and arcs, respectively, the objective of a Least-Cost Problem is to find the path from an origin node \(r\) to a destination node \(s\) that renders least possible cost, given that each arc \((i,j) \in A\) has a cost \(c_{ij}\).

Objective:

\[ \min_{\mathbf{x}} z = \sum_{(i,j)\in A} c_{ij}x_{ij} \]

Subject to:

\[\begin{split} \begin{aligned} \sum_{k \in H(r)} x_{rk} & = 1 \\ \sum_{k \in T(s)} x_{ks} & = 1 \\ \sum_{i \in T(j)} x_{ij} & = \sum_{k \in H(j)} x_{jk} & \ \forall \ j \in N \\ x_{ij} & \in \{0,1\} & \ \forall \ (i,j) \in A \\ \end{aligned} \end{split}\]

Here, \(T(i)\) represents the set of predecessor (tail) nodes of node \(i\), while \(H(i)\) represents the set of successor (head) nodes, defined as follows,

\[\begin{split} \begin{aligned} T(i) & = \{k; \ (k,i) \in A\} \\ H(i) & = \{k; \ (i,k) \in A\} \end{aligned} \end{split}\]

Note, \(x_{ij}\) represents traversal on arc \((i,j)\).

Example #1#

Consider the following network of El Dorado city. An individual residing in their home (#1) wishes to travel to their office (#6). Determine the least cost path from home to office for this indivudual.

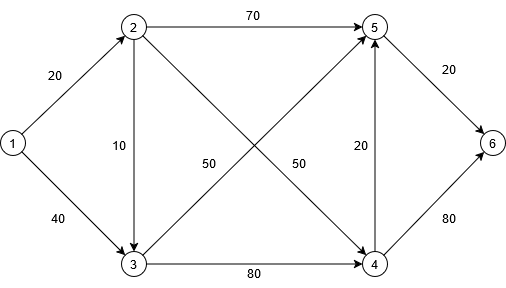
Figure 1. El Dorado City Network

From

To

Cost (₹)

1

2

20

1

3

40

2

3

10

2

4

50

2

5

70

3

4

80

3

5

50

4

5

20

4

6

80

5

6

20

  1. Formulate a linear optimisation model for this problem.

    Objective:

    \[ \min_{\mathbf{x}} z = 20x_{12} + 40x_{13} + 10x_{23} + 50x_{24} + 70x_{25} + 80x_{34} + 50x_{35} + 20x_{45} + 80x_{46} + 20x_{56} \]

    Subject to:

    \[\begin{split} \begin{aligned} x_{12} + x_{13} & = 1 \\ x_{12} & = x_{23} + x_{24} + x_{25} \\ x_{13} + x_{23} & = x_{34} + x_{35} \\ x_{24} + x_{34} & = x_{45} + x_{46} \\ x_{25} + x_{35} + x_{45} & = x_{56} \\ x_{46} + x_{56} & = 1 \\ x_{ij} & \in \{0,1\} & \ \forall \ (i,j) \in A \\ \end{aligned} \end{split}\]

  2. Solve the above linear optimisation model using a spreadsheet to find the optimal solution.

    The optimal path is 1-2, 2-3, 3-5, 5-6, rendering a total cost of ₹200.

Example #2#

Consider the complete grid-based network of El Dorado City connecting residential zones in the surubs to commercial zone in the city center via office districts surrounding it. Determine the shortest, fastest, and the most eco-friendly route

Figure 2. El Dorado Grid Network

  1. from a residential zone to the commercial zone

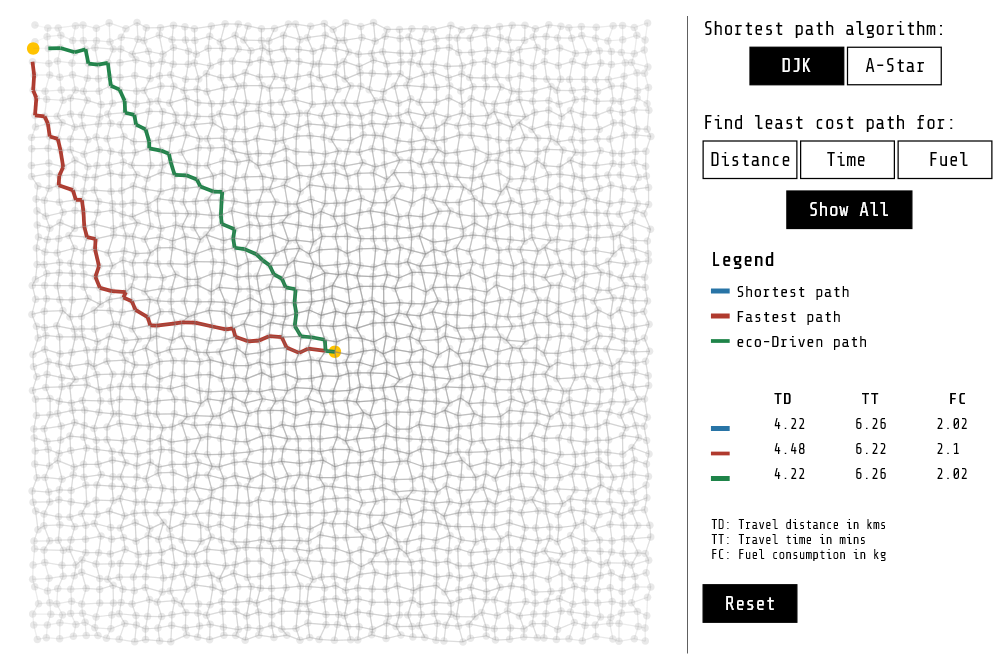
Figure 3. Routes from a residential zone to the commercial zone

  1. from a residential zone to an office district across the commercial zone

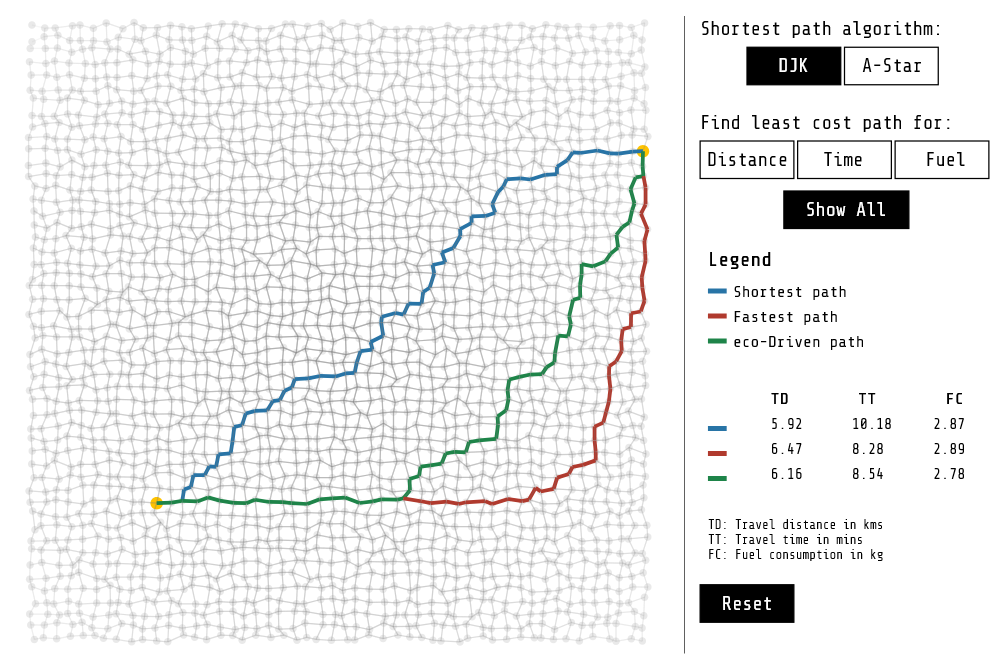
Figure 4. Routes from a residential zone to an office district across the commercial zone

  1. from one residential zone to another residential zone across the town

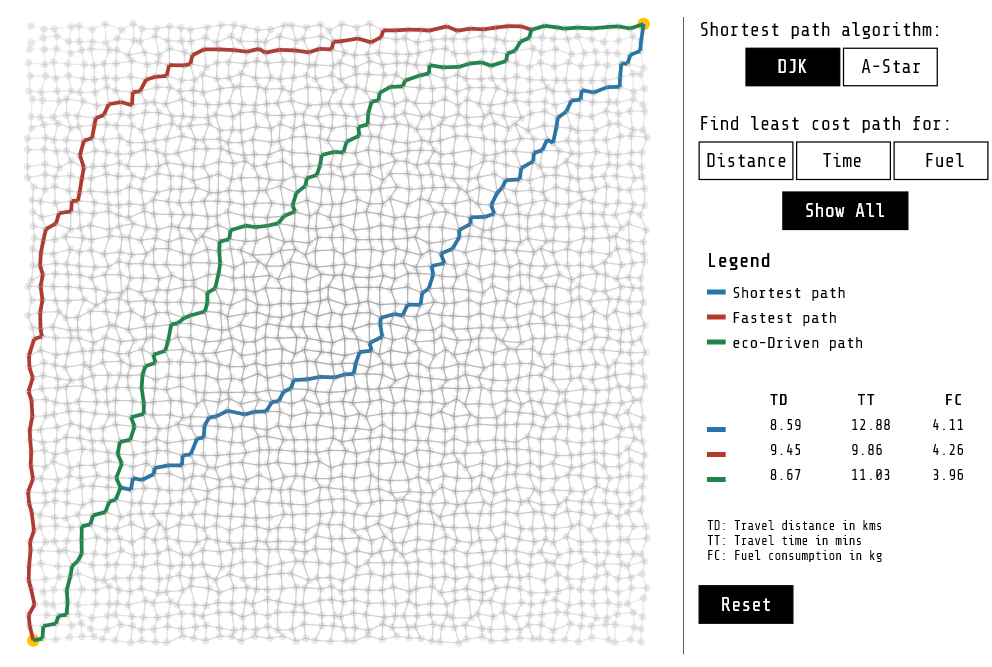
Figure 5. Routes from one residential zone to another residential zone across the town

Contents