Lecture 31: Single-Server Queueing Systems

Lecture 31: Single-Server Queueing Systems#

Note

This lecture details how to simulate a single-server queueing system laying foundations for multi-server queueing systems such as a Highway Toll Plaza. To this end, this lecture defines the problem and susbequently presents an example.

Problem Definition#

Consider a single-server queueing system initialized empty and idle \(\left(t = 0, j = 0 \ \text{and} \ \varphi = 0 \right)\). A customer \(i\) arrving at inter-arrival time \(a_i\), either waits in the queue if the server is busy \(\left(\varphi = 1 \right)\), incurring a delay of \(d_i\), or directly enters service spanning a duration of \(s_i\), if the server is idle. Note, here we assume customer inter-arrival and service times to be independently, identically, and randomly distributed.

Single-Server Queueing System
Figure: Illustration of a single-server queueing system

For this server, we are interested in the assessing following three performance metrics over a service of \(n\) customers spanning a total duration of \(t(n)\):

  • Average Customer Delay: \(d(n) = \sum_{i=1}^n d_i / n\)

  • Average Queue Length: \(q(n) = \sum_{j=1}^{\infty} jt_j / t(n)\), where \(t_j\) is the duration for which queue length is \(j\)

  • Average Server Utilization: \(u(n) = \)t_{\varphi = 1} / t(n)\(, where \)t_{\varphi = 1}$ is the duration for which the server is busy

Note, these performance metrics represent outcomes of a single simulation. Hence, to comprehensively assess this server, we evaluate measures of location, dispersion, and shape on the performance metrics across a large number of simulations.

Note

While customer inter-arrival and service times are independently, idenitically, and randomly distirbuted random variables, customer delay, queue length, and server status are not. Specifically, these random variables, and consequently, average customer delay, average queue length, as well as average server utilization depend on the actual realisation of customer inter-arrival and service times.

Example#

Consider a single-server queueing system with following inter-arrival times and service times.

\[\begin{split} A = [0.4, 1.2, 0.5, 1.7, 0.2, 1.6, 0.2, 1.4, 1.9] \\ S = [2.0, 0.7, 0.2, 1.1, 3.7, 0.6, 1.0, 1.0, 1.0] \end{split}\]

Calculate the average customer delay, average queue lenght, and average server utilization for 6 customers serviced by the server.

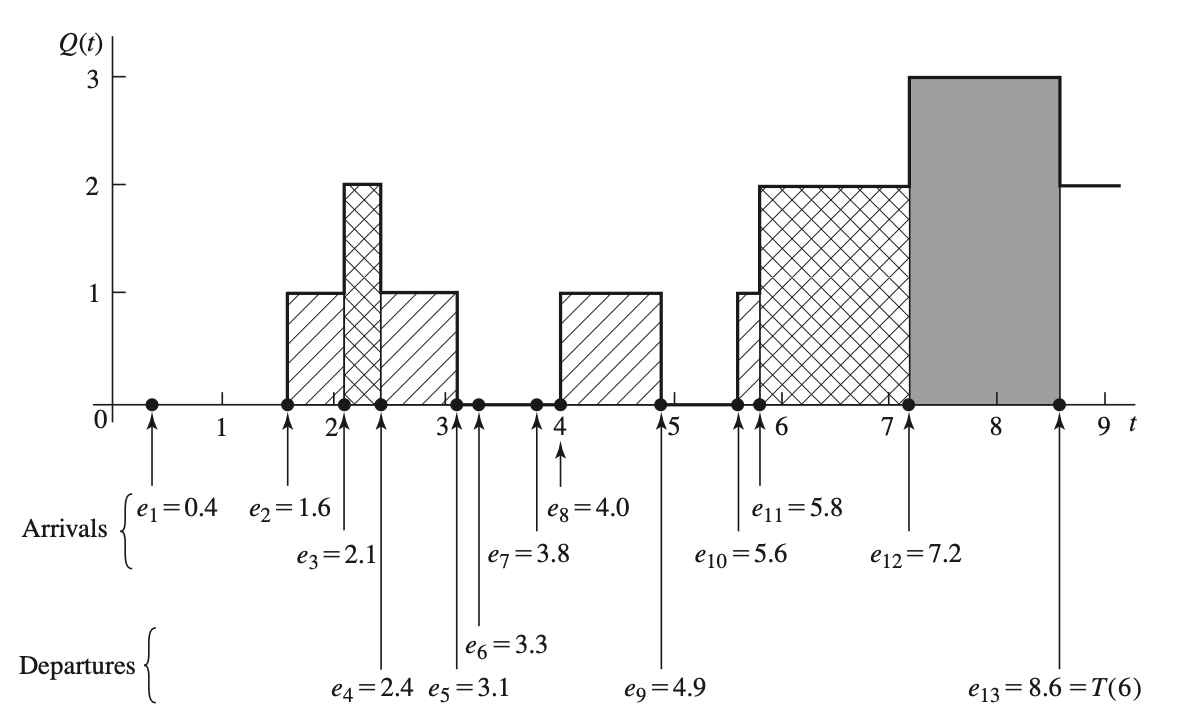
Single-Server Queueing System Exmaple
Figure: queue length, arrival times, and departure times for a realization of a single-server queueing system

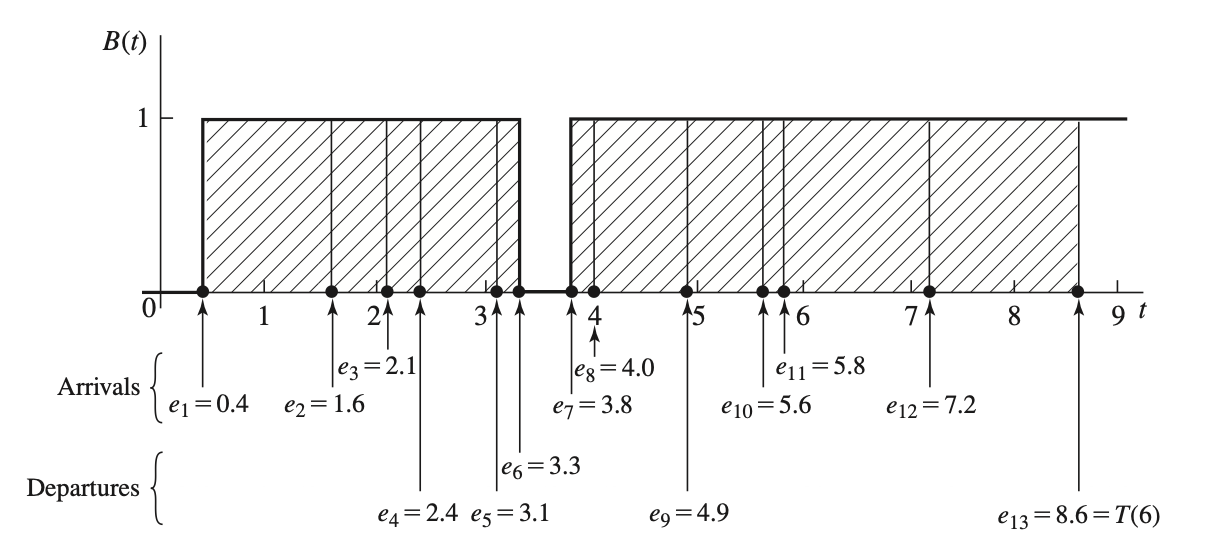
Single-Server Queueing System Example
Figure: server utilization, arrival times, and departure times for a realization of a single-server queueing system.

\[\begin{split} d = 0.950 \\ q = 1.217 \\ u = 0.902 \\ \end{split}\]

Note

In the next lecture, we will develop the simulation logic along with its implemenation in Python.

Contents