Lecture 27: Setting up Python#
Note
Python is an open-source, high-level, general-purpose programming language known for its simplicity and readability. Originally developed by Guido van Rossum in the late 1980s and first released in 1991, Python has since grown into one of the most popular programming languages for data analysis, machine learning, web development, automation, and scientific computing. Its strength lies in its extensive standard library, vibrant ecosystem of third-party packages, and ability to integrate seamlessly with other languages and tools.
Installing Python and JupyterLab / VS Code on Windows#
Follow these steps:
Step 1: Install Python#
Visit the official Python website: https://www.python.org/downloads/.
Download the latest stable version of Python (e.g., 3.x series) for Windows.
Run the installer:
Important: Check the box “Add Python to PATH” before clicking Install Now.
This ensures that Python commands can be run from the terminal.
Verify installation:
Open Command Prompt and type:
python --version
Step 2: Install VS Code#
Visit the official Visual Studio Code website: https://code.visualstudio.com/.
Download the Windows installer and run it.
During installation:
Select the option to add “Open with Code” to the right-click context menu.
Optionally, allow adding VS Code to the system PATH.
Launch VS Code after installation.
Step 3: Install the Python Extension for VS Code#
Open VS Code.
Go to the Extensions view (click the square icon on the left sidebar or press Ctrl+Shift+X).
Search for Python and install the extension published by Microsoft.
This extension adds syntax highlighting, IntelliSense, debugging, and Jupyter Notebook support.
Step 4: Install JupyterLab (Optional but Recommended)#
Open Command Prompt or VS Code Terminal and type:
pip install jupyterlabLaunch JupyterLab by typing:
jupyter lab
Once installed, open VS Code to begin writing Python code!
# Hello World in R
print("Hello World!")
Hello World!
Data Types in Python#
Python supports the following basic data types:
Character
Numeric
Integer
Logical
Complex
Here are some examples:
# Character
x = "CE5540"
print("Type of x is: ", type(x))
# Float
r = 3.14
print("Type of y is: ", type(r))
# Integer
v = int(42)
print("Type of v is: ", type(v))
# Logical
f = True
print("Type of f is: ", type(f))
# Complex
z = 2 + 3j
print("Type of z is: ", type(z))
Type of x is: <class 'str'>
Type of y is: <class 'float'>
Type of v is: <class 'int'>
Type of f is: <class 'bool'>
Type of z is: <class 'complex'>
Data Structures in Python#
Python supports the following data structures:
Vectors
Matrices
Lists
Data Frames
Here are some examples:
import numpy as np
import pandas as pd
# Vectors
v1 = ["Apple", "Banana", "Mango"]
v2 = [9, 1, 5, 4, 6, 7, 0, 3, 8]
v3 = list(range(1, 6)) # R's 1:5
print("# Vectors")
print(v1)
print(v2)
print(v3)
print(f"Accessing a value in a vector: v1[0] = {v1[0]}. \nNotice that Python uses 0-based indexing!")
# Matrices (NumPy arrays)
data = [9, 1, 5, 4, 6, 7, 0, 3, 8]
## By row
m1 = np.array(data).reshape(3, 3, order='C')
## By column
m2 = np.array(data).reshape(3, 3, order='F')
print("\n# Matrices")
print("m1 (by row):\n", m1)
print("m2 (by column):\n", m2)
print(f"Accessing a value in a matrix: m1[0, 2] = {m1[0, 2]}")
# Dictionaries
l = {"name": "John", "age": 25, "scores": [90, 85, 88]}
print("\n# Dict")
print(l)
print(f"Accessing a value in a dict: l['name'] = {l['name']}")
# Data Frames (pandas)
df = pd.DataFrame({"Name": ["Alice", "Bob"], "Age": [23, 25]})
print("\n# Data Frame")
print(df)
print(f"Accessing a value in a data frame: df['Age'].iloc[0] = {df['Age'].iloc[0]}")
# Vectors
['Apple', 'Banana', 'Mango']
[9, 1, 5, 4, 6, 7, 0, 3, 8]
[1, 2, 3, 4, 5]
Accessing a value in a vector: v1[0] = Apple.
Notice that Python uses 0-based indexing!
# Matrices
m1 (by row):
[[9 1 5]
[4 6 7]
[0 3 8]]
m2 (by column):
[[9 4 0]
[1 6 3]
[5 7 8]]
Accessing a value in a matrix: m1[0, 2] = 5
# Dict
{'name': 'John', 'age': 25, 'scores': [90, 85, 88]}
Accessing a value in a dict: l['name'] = John
# Data Frame
Name Age
0 Alice 23
1 Bob 25
Accessing a value in a data frame: df['Age'].iloc[0] = 23
Control Flow#
Here is how you would write control flow statements in Python
x = 10
if x > 0:
print("x is a positive number")
elif x < 0:
print("x is a negative number")
else:
print("x is zero!")
x is a positive number
Writing Loops in Python#
Python supports both for and while loops.
# For loop
print("# For Loop")
for i in range(1, 6): # range(1, 6) generates 1, 2, 3, 4, 5
print("Iteration:", i)
# While loop
print("\n\n# While Loop")
i = 1
while i <= 5:
print("Count:", i)
i = i + 1
# For Loop
Iteration: 1
Iteration: 2
Iteration: 3
Iteration: 4
Iteration: 5
# While Loop
Count: 1
Count: 2
Count: 3
Count: 4
Count: 5
Writing Functions in Python#
Functions are blocks of code that can be reused. Here’s how to define and call one.
# Factorial Function (Iterative Form)
def factorial_iterative(n):
result = 1
for i in range(2, n + 1): # range is end-exclusive, so use n+1
result *= i
return result
# Example usage
print(factorial_iterative(5)) # Output: 120
120
# Factorial Function (Recursive Form)
def factorial_recursive(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial_recursive(n - 1)
# Example usage
print(factorial_recursive(5)) # Output: 120
120
Summarising Data in Python#
In this segment of the lecture, we will develop measures of location, dispersion, and shape discussed in the previous lecture through 2024 ITUS sample individual dataset.
import pandas as pd
# 2024 ITUS Individual Data (original)
url = "https://raw.githubusercontent.com/anmpahwa/CE5540/refs/heads/main/resources/ITUS_IND_OG.csv"
data = pd.read_csv(url) # Loading Data
# Data structure
print(data.info())
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 533719 entries, 0 to 533718
Data columns (total 23 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 survey_year 533719 non-null int64
1 fsu_serial_no 533719 non-null int64
2 sector 533719 non-null int64
3 nss_region 533719 non-null int64
4 district 533719 non-null int64
5 stratum 533719 non-null int64
6 sub_stratum 533719 non-null int64
7 sub_round 533719 non-null int64
8 fod_sub_region 533719 non-null int64
9 nsc 533719 non-null int64
10 household_id 533719 non-null int64
11 individual_id 533719 non-null int64
12 response_code 533719 non-null int64
13 day_of_week 533719 non-null int64
14 type_of_day 533719 non-null int64
15 relation_to_head 533719 non-null int64
16 gender 533719 non-null int64
17 age 533719 non-null int64
18 marital_status 533719 non-null int64
19 education_level 533719 non-null int64
20 employment_status 533719 non-null int64
21 industry 533719 non-null int64
22 weight 533719 non-null float64
dtypes: float64(1), int64(22)
memory usage: 93.7 MB
None
# Filtering out into a smaller dataset
data = data[(data["nss_region"] == 241) & (data["employment_status"] == 81)]
# View the filtered data (head for preview)
print(data.head())
survey_year fsu_serial_no sector nss_region district stratum \
38 2024 30010 1 241 17 13
210 2024 30013 1 241 26 13
225 2024 30013 1 241 26 13
229 2024 30013 1 241 26 13
312 2024 30014 1 241 29 13
sub_stratum sub_round fod_sub_region nsc ... day_of_week \
38 11 2 2420 4 ... 1
210 10 1 2423 4 ... 4
225 10 1 2423 4 ... 7
229 10 1 2423 4 ... 7
312 11 4 2420 4 ... 7
type_of_day relation_to_head gender age marital_status \
38 1 5 1 22 1
210 1 5 1 18 1
225 1 6 1 18 1
229 1 5 1 19 1
312 1 5 1 35 1
education_level employment_status industry weight
38 10 81 99999 208857.0
210 5 81 99999 207000.0
225 5 81 99999 207000.0
229 4 81 99999 207000.0
312 2 81 99999 196571.0
[5 rows x 23 columns]
import pandas as pd
import numpy as np
from scipy import stats
# Measures of Location
z1 = data["age"].mean() # Mean
z2 = data["age"].median() # Median
z3 = data["age"].mode()[0] # Mode (returns Series, take first)
print("Mean:", round(z1, ndigits=3))
print("Median:", round(z2, ndigits=3))
print("Mode:", round(z3, ndigits=3))
# Measures of Dispersion
z1 = data["age"].max() - data["age"].min() # Range
z2 = stats.iqr(data["age"], nan_policy="omit") # IQR
z3 = data["age"].std() # Standard deviation
print("Range:", round(z1, ndigits=3))
print("IQR:", round(z2, ndigits=3))
print("SD:", round(z3, ndigits=3))
# Measures of Distribution
z1 = stats.skew(data["age"], nan_policy="omit") # Skewness
z2 = stats.kurtosis(data["age"], nan_policy="omit") # Kurtosis (Fisher's definition)
print("Skewness:", round(z1, ndigits=3))
print("Kurtosis:", round(z2, ndigits=3))
Mean: 26.949
Median: 23.0
Mode: 18
Range: 70
IQR: 11.0
SD: 11.423
Skewness: 1.816
Kurtosis: 4.337
Linear Regression in Python#
# Load necessary libraries
import pandas as pd
import seaborn as sns
import statsmodels.api as sm
import matplotlib.pyplot as plt
# Notebook/plot display options
plt.rcParams['figure.figsize'] = (9, 6)
pd.set_option('display.max_columns', None) # Optional: show all columns when printing
# 2024 ITUS Individual Data (original)
url = "https://raw.githubusercontent.com/anmpahwa/CE5540/refs/heads/main/resources/ITUS_HHD_DT.csv"
data = pd.read_csv(url)
# Data structure
print(data.info())
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 139487 entries, 0 to 139486
Data columns (total 21 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Unique_HH_ID 139487 non-null object
1 time_of_year 139487 non-null int64
2 day_of_week 139487 non-null int64
3 sector 139487 non-null int64
4 region 139487 non-null int64
5 district_population 139487 non-null int64
6 gender_ratio 139487 non-null float64
7 average_age 139487 non-null float64
8 marital_status 139487 non-null int64
9 highest_eduLevel 139487 non-null int64
10 employment_ratio 139487 non-null float64
11 family_structure 139487 non-null float64
12 household_size 139487 non-null int64
13 religion 139487 non-null int64
14 social_group 139487 non-null int64
15 land_possessed 139487 non-null int64
16 total_expenditure 139487 non-null int64
17 dwelling_unit 139487 non-null int64
18 dwelling_structure 139487 non-null int64
19 weight 139487 non-null int64
20 shopping_choice 139487 non-null int64
dtypes: float64(4), int64(16), object(1)
memory usage: 22.3+ MB
None
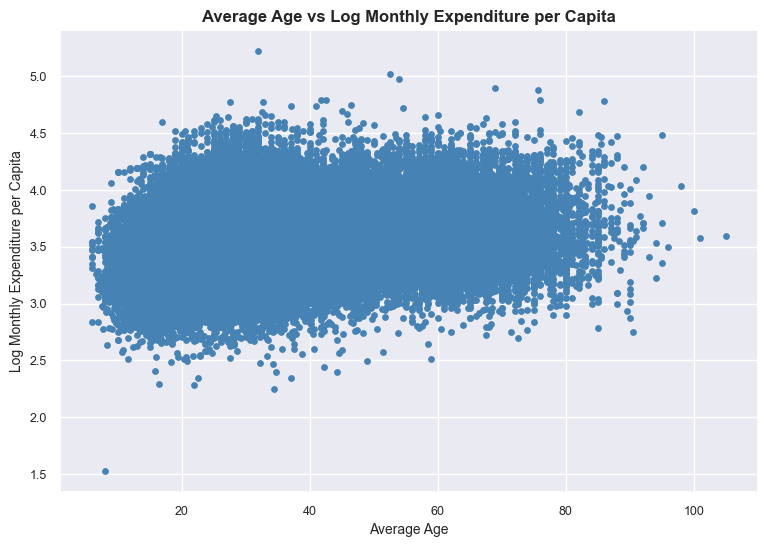
Scatter Plot#
# Scatter Plot
plt.scatter(
data["average_age"],
np.log10(data["total_expenditure"] / data["household_size"]),
color="steelblue",
s=15 # matches your earlier size=2 in ggplot (Matplotlib uses points^2)
)
plt.title("Average Age vs Log Monthly Expenditure per Capita", fontsize=12, fontweight="bold")
plt.xlabel("Average Age", fontsize=10)
plt.ylabel("Log Monthly Expenditure per Capita", fontsize=10)
plt.xticks(fontsize=9)
plt.yticks(fontsize=9)
plt.show()
# Compute Pearson correlation
correlation = data["average_age"].corr(np.log10(data["total_expenditure"] / data["household_size"]))
print("Correlation between average age and monthly expenditure:", round(correlation, 3))
Correlation between average age and monthly expenditure: 0.264
# Define variables
X = data["average_age"]
y = np.log10(data["total_expenditure"] / data["household_size"])
# Fit linear regression model
X = sm.add_constant(X)
model = sm.OLS(y, X, missing="drop").fit()
# Display summary
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.070
Model: OLS Adj. R-squared: 0.070
Method: Least Squares F-statistic: 1.047e+04
Date: Sun, 10 Aug 2025 Prob (F-statistic): 0.00
Time: 16:16:59 Log-Likelihood: -1697.0
No. Observations: 139487 AIC: 3398.
Df Residuals: 139485 BIC: 3418.
Df Model: 1
Covariance Type: nonrobust
===============================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------
const 3.3684 0.002 2060.789 0.000 3.365 3.372
average_age 0.0046 4.52e-05 102.317 0.000 0.005 0.005
==============================================================================
Omnibus: 4880.760 Durbin-Watson: 0.757
Prob(Omnibus): 0.000 Jarque-Bera (JB): 6665.938
Skew: 0.374 Prob(JB): 0.00
Kurtosis: 3.767 Cond. No. 90.2
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
# Errors
# Sums of squares
sst = np.sum((np.asarray(model.model.endog) - np.asarray(model.model.endog).mean())**2) # total
ssr = np.sum((np.asarray(model.fittedvalues) - np.asarray(model.model.endog).mean())**2) # regression
sse = np.sum((np.asarray(model.model.endog) - np.asarray(model.fittedvalues))**2) # error
# Degrees of freedom
n = int(model.nobs)
p = int(model.df_model) + 1 # number of parameters incl. intercept
df_resid = int(model.df_resid)
# Metrics
rse = np.sqrt(sse / df_resid)
R2 = ssr / sst
AdjR2 = 1 - (1 - R2) * (n - 1) / (n - p)
print("SST :", round(sst, 2))
print("SSR :", round(ssr, 2))
print("SSE :", round(sse, 2))
print("RSE :", round(rse, 2))
print("R-squared :", round(R2, 3))
print("Adjusted R-squared:", round(AdjR2, 3))
SST : 8996.15
SSR : 628.05
SSE : 8368.1
RSE : 0.24
R-squared : 0.07
Adjusted R-squared: 0.07
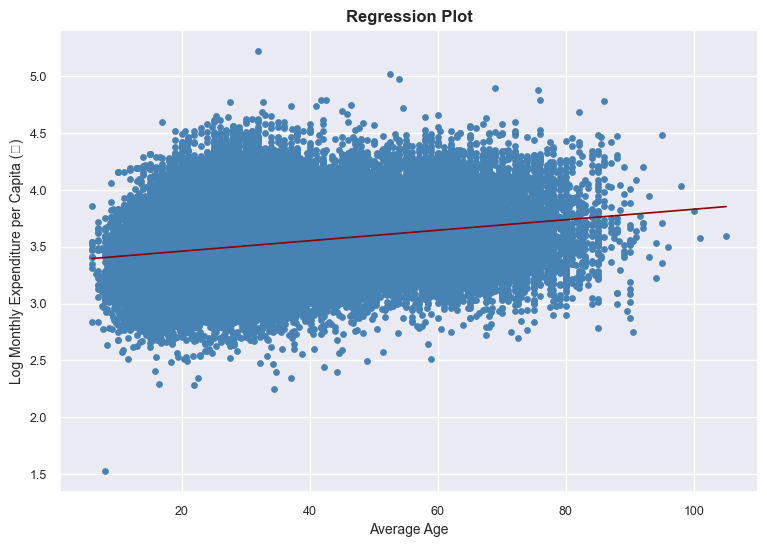
# Define variables
x = data["average_age"]
y = np.log10(data["total_expenditure"] / data["household_size"])
# Fit simple linear regression y = m*x + b
m, b = np.polyfit(x, y, 1)
# Regression line for plotting
x_line = np.linspace(x.min(), x.max(), 200)
y_line = m * x_line + b
# Scatter
plt.scatter(x, y, color="steelblue", s=15)
# Regression line (no CI, like se = FALSE)
plt.plot(x_line, y_line, color="darkred", linewidth=1.2)
# Labels & styling
plt.title("Regression Plot", fontsize=12, fontweight="bold")
plt.xlabel("Average Age", fontsize=10)
plt.ylabel("Log Monthly Expenditure per Capita (₹)", fontsize=10)
plt.xticks(fontsize=9)
plt.yticks(fontsize=9)
plt.show()
/Users/anmolpahwa/Library/Python/3.13/lib/python/site-packages/IPython/core/pylabtools.py:170: UserWarning: Glyph 8377 (\N{INDIAN RUPEE SIGN}) missing from font(s) Arial.
fig.canvas.print_figure(bytes_io, **kw)
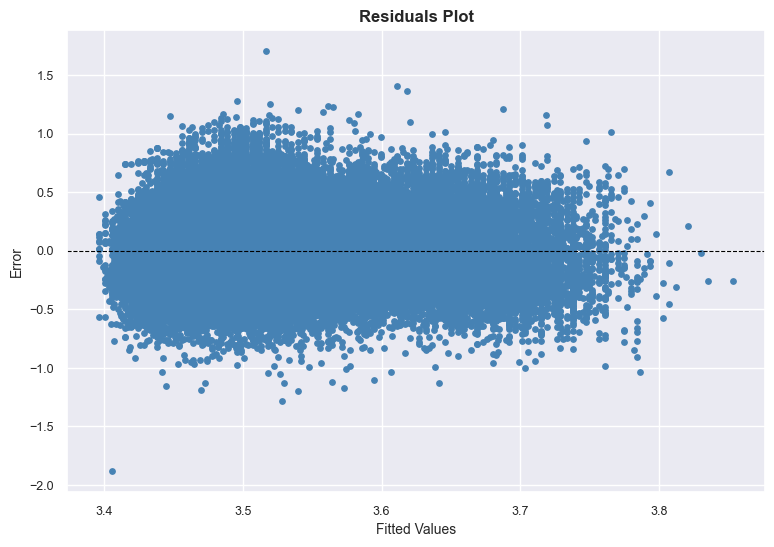
# Extract fitted values and residuals from statsmodels model
fitted_vals = model.fittedvalues
residuals = model.resid
# Scatter plot of residuals vs fitted values
plt.scatter(fitted_vals, residuals, color="steelblue", s=15)
# Add horizontal zero reference line
plt.axhline(y=0, color="black", linestyle="--", linewidth=0.8)
# Labels & styling
plt.title("Residuals Plot", fontsize=12, fontweight="bold")
plt.xlabel("Fitted Values", fontsize=10)
plt.ylabel("Error", fontsize=10)
plt.xticks(fontsize=9)
plt.yticks(fontsize=9)
plt.show()